たし算・ひき算の筆算は、「一の位（正確には小数の計算もあるので末位）から計算する」という算数指導を根本的に問い直すことは、現時点ではご法度ですが、私はもう少し幅をもったらよいと考えています。そうすることで、理解が促進される子がいるだろうなあと思っているのですが、なかなか小学３年生までの加減乗除の指導が一通り終わるまではちょっと手が出せないと感じますので、小学４年生以降の概数を扱う頃から少しずつ「頭位（大きな数）」からの筆算を入れてみてはと思います。
実は、こうした研究は、1970年代から横地清氏や町田彰一郎氏などが中心となって行われており、「バラ数」と呼ばれているのですが、なかなか普及していないのが実情です。ただ、これだけ電子計算機が当たり前のように溢れ、浸透した世の中にあっては、1の位からしか絶対だめといった旧態依然した方法だけに固執するのは、そろそろ見直してはどうでしょうか。そろそろ、答えを予測する能力や、電卓等で求めた答えが妥当であるかをチェックする能力の育成にもう少し軸足を置いてはどうかと思います。
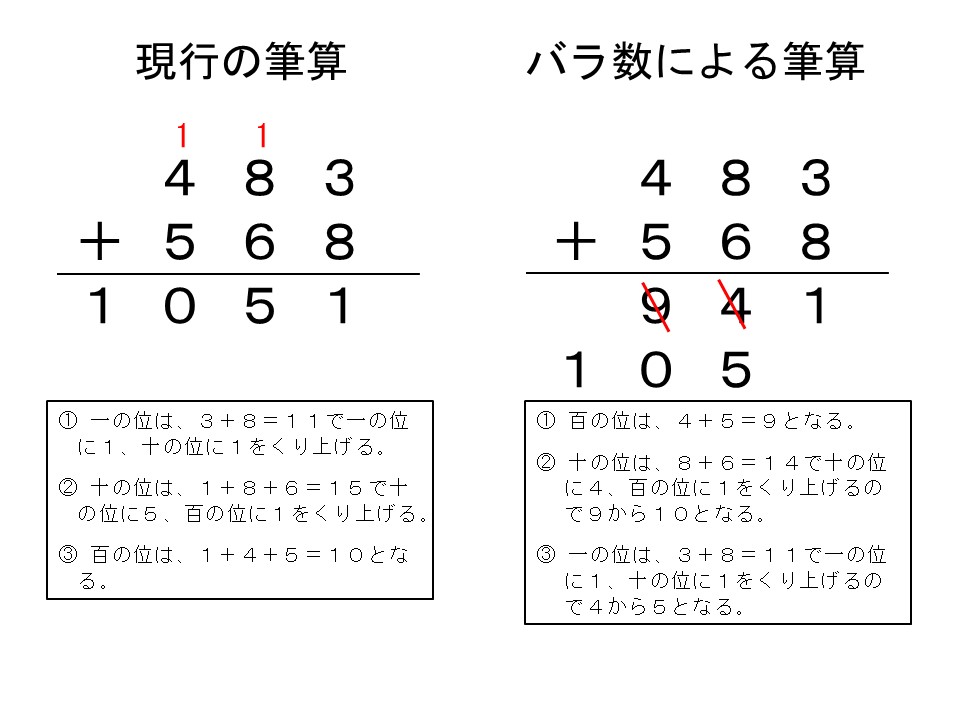
たとえば、写真①の左側の現行の筆算でのくり上がりのたし算では、３＋８をして１１の１は一の位、１は十の位に置きます。続いて、十の位では１＋８＋６と三つの数の計算とレベルが少し上がります。さらに百の位まで、三つの数の計算が続きます。一方、写真①の右側は「バラ数」計算で、頭位からの計算をしています。基本的には、二つの数の計算の組み合わせで解くことができます。求めた数字に斜線を入れるなど、面倒なところはあるのですが、それだけ作業が細分化されているということなので、理解が容易でない子には、効果的な面もあると考えています。
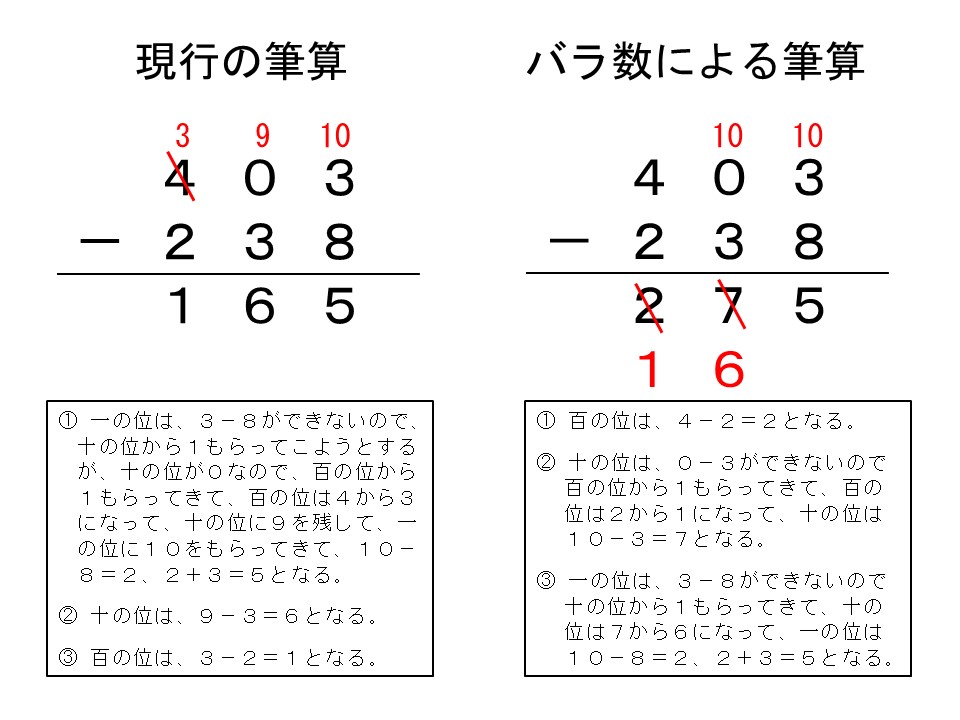
次に、くり下がりがあって、数字の間に０がある一番難しいとされるひき算を見てみます。写真②の左側の現行の筆算では、一の位のひき算ができないために、十の位と百の位まで見渡さなくてはならず、それぞれの位での動きが9になったり10になったりと、非常に複雑になっています。一方、写真②の右側では頭位からの計算をしていますので、基本的には、当該の位とその一つ上の位を考えるだけで問題が解けます。繰り返しになりますが、理解が容易でない子は、複数の手順を同時に求めるときに、不適応を生じがちですので、個々の手順を細分化してあげることでクリアしやすくしてあげて、学年が上がればそのことが当たり前のようにできるようになるという道順を踏んであげることが大切であると感じています。
写真①：くり上がりのあるたし算の筆算、写真②：くり下がりのあるひき算の筆算
投稿者プロフィール
-
大阪教育大学卒業，大阪教育大学大学院修士課程修了，大阪大学大学院博士後期課程修了。博士（人間科学）。
大阪府内の公立小学校勤務８年の後，佛教大学専任講師，助教授，准教授，教授を経て，現在，京都教育大学教育学部教授。
京都教育大学では，小学校教員養成，中・高等学校（数学）教員養成に従事。近年の研究テーマは「生成ＡＩを用いた算数・数学教育」。
小学校勤務時代，クラスで豚を飼うといった取り組みを３年間実践。フジテレビ「今夜は好奇心」にて1993年７月放映。第17回動物愛護映画コンクール「内閣総理大臣賞」受賞，第31回ギャラクシー賞テレビ部門「ギャラクシー奨励賞」受賞。2008年には『ブタがいた教室』として映画化。
コロナ禍の中で、日本語及び多言語に対応した算数・数学動画教材約3,300本を制作・公開した取り組みにより、2022年第7回IMS Japan賞優秀賞受賞、2023年第3回SDGsジャパンスカラシップ岩佐賞（教育の部）受賞、2023年日本民間放送連盟賞（特別表彰 青少年向け番組）最優秀賞受賞した。
著書に，「豚のＰちゃんと３２人の小学生」（ミネルヴァ書房），「脳科学の算数・数学教育への応用」（ミネルヴァ書房），編著に「初等算数科教育法序論」（共立出版），「オリガミクスで算数・数学教育」（共立出版）などがある。
最新の投稿
教育全般2025年3月3日【告知】2025年2月16日：黒田恭史・葛城元編著『オリガミクスで算数・数学教育』の先行予約始まりました！- 教育全般2025年3月3日【議論⑤（了）】2025年2月5日：『無藤隆先生の隠居感想「1／2と1／3はどちらが大きいか？」という問題が私には分からない』に応えて！
- 教育全般2025年3月3日【議論④】2025年2月4日：『無藤隆先生の隠居感想「1／2と1／3はどちらが大きいか？」という問題が私には分からない』に応えて！
- 教育全般2025年3月3日【議論③】2025年2月3日：『無藤隆先生の隠居感想「1／2と1／3はどちらが大きいか？」という問題が私には分からない』に応えて！
