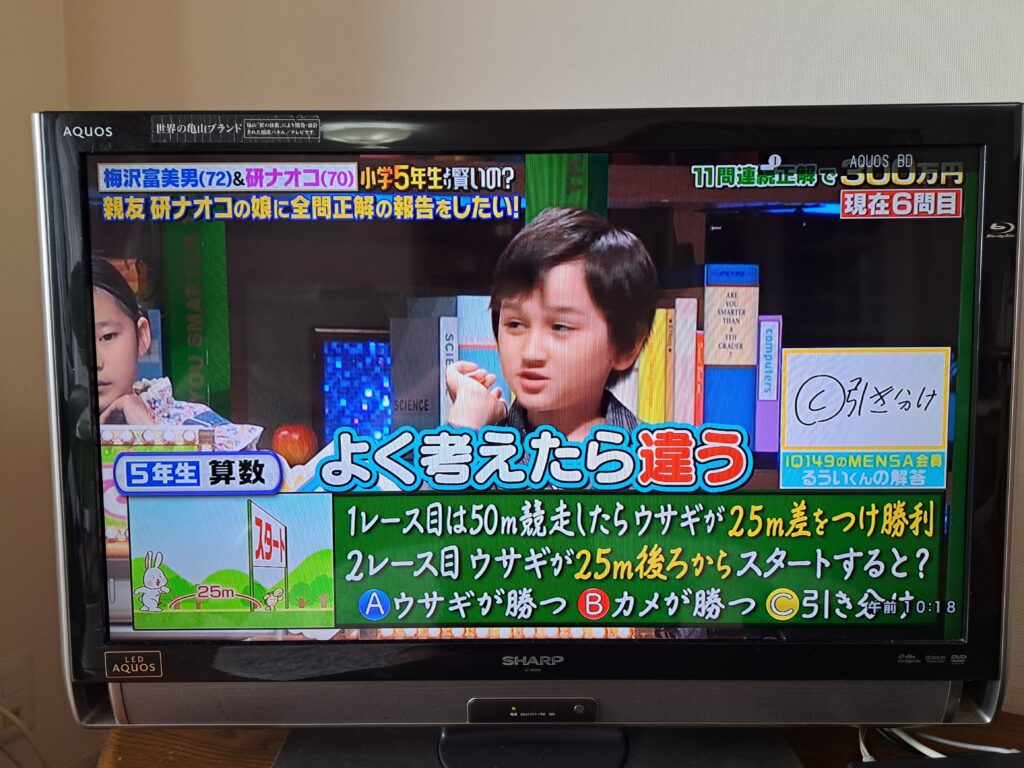
番組の中で、るういさんが途中で意見を変えます。最初は「引き分け」だったのですが、「速さが一緒だったら差が同じになるけど、速さが違うからウサギが勝つ」に変更したのです。これは、速さというものを加減の仕組みから乗除の仕組み（比）へと見方を転換するということで、非常に高度な思考が働いており、感心しました。
さて、私は子どもの速さに関する原初的なイメージは、瞬間の速さにあると思っています。子どもたちは、自分の目の前を凄いスピードで何かが走り去ったり、突然速くなったり遅くなったりするといった経験を積んできていますので、むしろ瞬間の速さが先にあると思います。
しかし、この瞬間の速さを数学的に数値化するためには、かなり高度な数学が必要となります。そこで、小学校では、速さ＝道のり÷時間という、平均の速さで定義づけています。その結果、少し厳しい言い方になるかもしれないのですが、子どもの速さに関する躍動感のある「動的認識」が、速さの公式という「静的認識」へ封じ込まれた感じがするのです。
こうなってしまうと、道のり、時間、速さという3要素の内の2つの要素が示されて、残りの1つの要素の数値を求めるための最適公式は何かということだけに関心が向いてしまいがちです。徒競走で相手を必死で追いかけ、追いつけるかどうか？といった、速さ本来の持つ醍醐味は影をひそめてしまうのです。
では、小学生の段階で、瞬間の速さの一部を感じ取る取り組みはできないのでしょうか。ＩＣＴの活用はその可能性を大きく引き出してくれます。例えば50m走を調べるとします。最初は、0～50mでタイムを計ります。続いて、0～25ｍと、25～50mに分けてタイムを計ります。現在のタブレットは、様々な機能を持ち備えていますので、こうした活動を子どもたちがペアになって、交互に実測することができます。続いて、0～10m、10～20m、･･･、40～50mで計ります。そうすると、0～10mはスタートなので時間がかかるとか、30～40mの時に一番タイムが短いので速いとか、40～50mは少しばてるので遅くなるといったことがわかってきます。逆に、高速連続撮影機能などを用いれば、1秒毎に進んだ距離を可視化することもできます。
なるほど、速さの公式は、これら全体を慣らして、平均の速さを求めるものだけど、短い区間で区切れば、瞬時、瞬時の正確な速さがわかるといった認識が芽生えれば大成功です。ICT機器を活用することで、既存の速さの学習が効果的にわかるだけでなく、これまで扱うことのできなかった瞬間の速さの一端に触れることができるわけです。
このような体験を積んでおけば、中学校理科の物理分野で扱う、等速運動や等加速度運動も連動してくるのではないかと思います。さらに、高校2年生の数学で学習する微分とは、限りなくこの区間を短くしたものということです。ちなみに、高校物理で重力加速度gというものを使って、物体の落下距離（1/2・gt^2）、落下スピード（gt）、落下（重力）加速度(g)を扱いますが、これはまさに、tを順に微分していったものです。落下「距離」の区間を限りなく微細に分けて分析すると、正確な落下「スピード」が出てくるという仕組みです（ちょっとややこしすぎました）。（終了）
投稿者プロフィール
-
大阪教育大学卒業，大阪教育大学大学院修士課程修了，大阪大学大学院博士後期課程修了。博士（人間科学）。
大阪府内の公立小学校勤務８年の後，佛教大学専任講師，助教授，准教授，教授を経て，現在，京都教育大学教育学部教授。
京都教育大学では，小学校教員養成，中・高等学校（数学）教員養成に従事。近年の研究テーマは「数学教育と脳科学」の学際的研究。
小学校勤務時代，クラスで豚を飼うといった取り組みを３年間実践。フジテレビ「今夜は好奇心」にて1993年７月放映。第17回動物愛護映画コンクール「内閣総理大臣賞」受賞，第31回ギャラクシー賞テレビ部門「ギャラクシー奨励賞」受賞。
著書に，「豚のＰちゃんと３２人の小学生」（ミネルヴァ書房），「脳科学の算数・数学教育への応用」（ミネルヴァ書房），編著に「数学科教育法入門」（共立出版）などがある。
