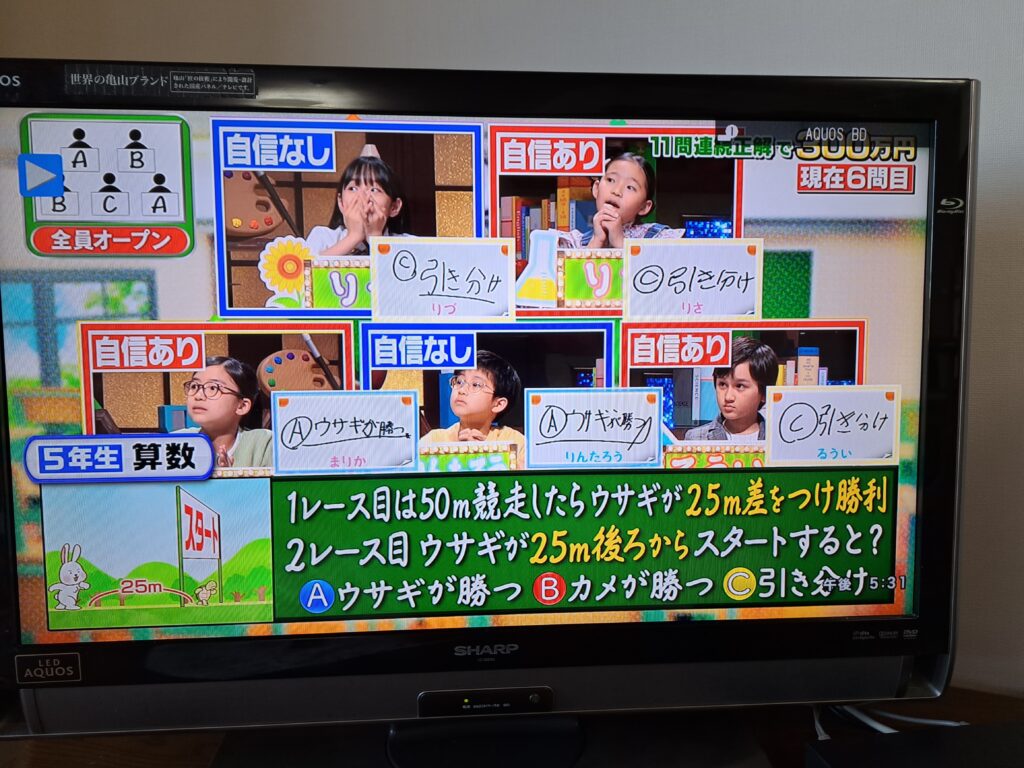
今回のテレビ放送では、5人の助っ人小学生の内、2人が正解の「ウサギが勝つ」で、3人が不正解の「引き分け」と解答しました（後で、1人がウサギが勝つに変更しました）。これを見ていて、速さの公式に簡単に持ち込めず、区間ごとの両者の位置関係を踏まえながら速さを考える問題は、やはり苦戦するんだなあと改めて思いました。
さて、前回は速さ指導のポイントとして、区間を様々に変化させて、どのように進むのかという特徴を考えさせることを指摘しました。今回は、平均の速さと瞬間の速さを話題にしながら、なぜ区間を様々に変化させることが重要なのかについて考えていきたいと思います。
小学校の算数教科書での速さの定義は、次の通りです。
「速さは、次の式で求めることができます。速さ＝道のり÷時間」
これは、正確には「平均の速さ」の定義と言えます。つまり、8kmの道のりを2時間で進んだ場合、8÷2＝4、時速4kmとなりますが、途中で少し急いで進んだり、最後の方は疲れてゆっくりになったとしても、結局8kmを2時間で進めば、時速4kmは変わらないので、平均した速さということになるのです。
もう一つの速さに「瞬間の速さ」があります。車のスピードメータがそれです。加速したり減速したりすると、時速がどんどんと変化していきますが、これは瞬間の速さを数値化しています。従って、先の8kmを2時間で進む場合も、スマートウオッチなどを装着していれば、瞬間の速さの変化が刻々とわかるようになります。ただし、この瞬間の速さを数学を用いて数値化するためには、高校2年生数学の微分の考えを用いますので、かなり高度な数学が必要となります。
実は小学校算数の教科書には、平均の速さだけでなく瞬間の速さが、知らず知らずの内に登場しています。「時速4kmで2時間進みました。何km進みましたか？」という問題の、最初に出てくる時速4kmというのは、実は瞬間の速さの意味で用いています。すなわち、どの時点を切り取っても、時速4kmという一定の速さで進んでいますので、これは平均ではなく瞬間の速さとなるわけです。
ですので、道のりを細かく区切って考えてみると、同じ時速4kmという値であったとしても、平均の速さの場合と瞬間の速さの場合で異なることになるのです。もちろん、こうした議論は小学校では扱いませんが、私はとても大切であると考えています。
次回は、様々な区間で区切って考えることの大切さについて解説します。
投稿者プロフィール
-
大阪教育大学卒業，大阪教育大学大学院修士課程修了，大阪大学大学院博士後期課程修了。博士（人間科学）。
大阪府内の公立小学校勤務８年の後，佛教大学専任講師，助教授，准教授，教授を経て，現在，京都教育大学教育学部教授。
京都教育大学では，小学校教員養成，中・高等学校（数学）教員養成に従事。近年の研究テーマは「数学教育と脳科学」の学際的研究。
小学校勤務時代，クラスで豚を飼うといった取り組みを３年間実践。フジテレビ「今夜は好奇心」にて1993年７月放映。第17回動物愛護映画コンクール「内閣総理大臣賞」受賞，第31回ギャラクシー賞テレビ部門「ギャラクシー奨励賞」受賞。
著書に，「豚のＰちゃんと３２人の小学生」（ミネルヴァ書房），「脳科学の算数・数学教育への応用」（ミネルヴァ書房），編著に「数学科教育法入門」（共立出版）などがある。
最新の投稿
教育全般2024年5月12日【質問】「資質・能力を育成する」という言葉遣いへの違和感- 教育全般2024年4月7日【提案】学校における「プロボノ」精神の浸透を
- 教育全般2024年4月7日【提案】非認知能力をめぐって⑥ 「非認知能力」と「学級づくり」の関係
- 教育全般2024年4月7日【提案】非認知能力をめぐって⑤ そろそろ「非認知能力」という言葉を使うのをやめて「社動（シャドウ）スキル」と言いませんか
